在本文中我们将实现经典的基于首次适应类型的 malloc. 首次适应算法很简单:遍历块链表,当找到满足请求大小并且是free标记的块的时候停止。
1. 指针对齐
通常指针被要求与整型类型对齐 (也即是指针类型大小), 在案例中只考虑32位的情况。于是我们的指针必须是4的倍数 (32 bits = 4 bytes) 因为我们的meta-data块已经对齐,现在唯一要做的是对齐数据块(data block)。
本文地址:http://wuyudong.com/2016/07/30/2372.html,转载请注明源地址。
如何实现呢? 有几种方法,其中比较高效的是增加一个使用算术技巧的预处理宏。
算术技巧: 给定任何的正整数n被4做整数除法,然后乘以4,结果为最接近n且比n小的4的倍数,为了获得最接近n且比n大的4的倍数,只需要在得到的结果上加上4,这个很简单,但是对于n本身为4的倍数的情况不适用,因为这样操作的结果将是4的另一个倍数.
但是,再一次依据算术:
假设x是一个整数,可以表示成 x = 4 × p + q,其中 0 ≤ q ≤ 3,
如果 x 是4的倍数, q = 0 且x−1 = 4×(p−1)+3,于是((x−1)/4)×4+4 = 4× p = x.
如果x 不是4的倍数, 于是 q , 0 and x − 1 = 4 × p + (q − 1) 与0 ≤ q − 1 ≤ 2,于是 (x−1)/4×4+4 = 4× p+4 = x/4×4+4.
我们有表达式 (x−1)/4×4+4 总能得到大于或等于最接近4的倍数.
但是怎样用C语言实现呢 ? 首先,注意到乘以和除以4可以使用比一般运算更快的左移和右移位操作 (C中的>> 和 << ) , 于是我们的式子可以写成C语言的形式为: (((x-1)>>2)<<2)+4,为了防止错误我们需要加上额外的括号:
(((((x)-1)>>2)<<2)+4),现在我们可以写出下面的宏:
#define align4(x) (((((x)-1)>>2)<<2)+4)
2. 查找块:首次适应算法
找到一个足够大的空闲(free)块相当的容易:我们从堆的基地址(base) (在代码中以某种形式记录下来,我们后面用得着)检测当前块,如果满足我们的请求直接将其地址返回,否则继续下一块直到找到一个合适的块或者到达尾部的头地址。 唯一的技巧是保持最后访问的块,于是当我们找不到合适块的时候malloc函数可以很容易扩展堆。代码很简单,base是一个指向堆的起始部位的全局指针:
t_block find_block(t_block *last, size_t size)
{
t_block b = base;
while (b && !(b->free && b->size >= size)) {
*last = b;
b = b->next;
}
return (b);
}
这个函数返回满足条件的块,或者如果没有找到返回NULL,在没有找到的情况下,参数last指向最后访问的块(chunk).
3. 扩展堆
我们并不是总能找到匹配的块,并且有时我们需要扩展堆,这很简单:我们移动 break并初始化一个新的块(block),当然我们需要更新堆中的最后一个块的next域。在后面的开发中,我们需要使用一些技巧在block的结构体上,于是定义一个宏保存meta-data块的大小:
#define BLOCK_SIZE sizeof(struct s_block)
如果sbrk执行失败则返回 NULL,注意到我们不确定 sbrk 返回break的前驱块,我们最初保存它然后移动break,可以通过last 与last->size来计算它
t_block extend_heap(t_block last, size_t s)
{
t_block b;
b = sbrk(0);
if (sbrk(BLOCK_SIZE + s) == (void *)-1)
/* sbrk失败,返回NULL */
return (NULL);
b->size = s;
b->next = NULL;
if (last)
last->next = b;
b->free = 0;
return (b);
}
4. 分割块
您可能已经注意到,我们使用第一个有效可用块,不顾它的大小(提供足够大),如果这样做后面将释放很多的空间(试想:如果请求2个字节但是找到一个256字节的块),第一个解决办法是划分块:当一个块空间的大小足够满足要求,可以随后产生一个新的块 (至少为BLOCK SIZE + 4), 我们往链表中插入一个新的块.
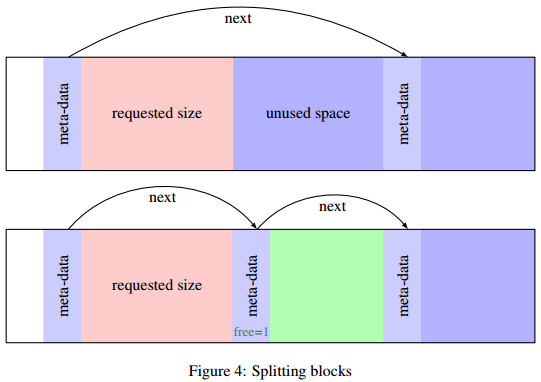
接下来的函数仅在空间有效的时候被调用,提供的块的大小同样需要对齐。 在这个函数中,我们将做一些指针运算,为了避免错误,将使用一点技巧来保证我们的操作精确到1字节 (注意 p+1 取决于p指向的类型)
我们将块结构体添加另一个域,一个字符数组。该数组的指针指向meta-data块的尾部。 C语言禁止出现0长度数组,于是我们定义一个长度为1的数组。(ps:这样的数组称为柔性数组,我的博客中有专门的文章介绍)
struct s_block {
size_t size;
t_block next;
int free;
char data[1];
};
/* 更新 BLOCK_SIZE 宏 */
#define BLOCK_SIZE 12 /* 3*4 ... */
注意到这种扩展并不需要在扩展的堆上作任何的修改,因为新的域不能直接使用.
现在实现分割块: 这个函数通过传递的参数来切断块,从而实现要求大小的数据块(data block),Figure 4显示了整个操作过程。
void split_block(t_block b, size_t s)
{
t_block new;
new = b->data + s;
new->size = b->size - s - BLOCK_SIZE;
new->next = b->next;
new->free = 1;
b->size = s;
b->next = new;
}
注意到第4行使用 b->data进行指针算术运算,因为data域是字符型数组 char[] ,我们可以肯定那个求和运算是按照字节精度完成.
5. malloc函数
现在可以实现我们的malloc了,它几乎就是对之前实现的函数的一个封装,我们必须对齐请求的大小,判断是否是第一次调用malloc函数,并且其他的条件是否被告知。记住之前函数查找块的时候使用了一个全局变量base,这个变量定义如下:
void *base=NULL;
它是空指针并被初始化为 NULL,我们的malloc首先要做的事就是测试base,如果为NULL,这是我们第一次调用,否则我们使用之前描述的算法。
按照下面的步骤实现malloc:
• 首先对齐请求的块大小;
• 如果base已经初始化:
– 查找一个足够大的空闲块;
– 如果我们找到一个块:
* 尝试分割块 (请求块的大小和已知块的大小的差距是meta-data块和最小4字节的块;
* 标记块已经在使用中 (b->free=0);
– 否则: 扩展堆.
注意last的使用: find_block使用一个指针指向最后访问的块(chunk), 这样我们就
可以在扩展堆的时候访问它,而不需要去遍历整个链表.
• 否则: 扩展堆 (这时指针为空)
注意,我们扩展堆的函数是使用last=NULL.
同样要注意到每次执行失败,我们都按照malloc的规范返回NULL,下面是malloc 函数的代码:
void *malloc(size_t size)
{
t_block b, last;
size_t s;
/* 对齐 */
s = align4(size);
if (base) {
/* 查找第一个block */
last = base;
b = find_block(&last, s);
if (b) {
/* 判断能否分割块 */
if ((b->size - s) >= (BLOCK_SIZE + 4))
split_block(b, s);
b->free = 0;
} else {
/* 没有合适的块,扩展堆 */
b = extend_heap(last, s);
if (!b)
return (NULL);
}
} else {
/* 第一次 */
b = extend_heap(NULL, s);
if (!b)
return (NULL);
base = b;
}
return (b->data);
}


Comments